Researchers in the robotics laboratory at ETH and for sure other universities were struggling with the complicated, not-efficient simulators for rigid and viscoelastic materials in multi-body systems to implement their ideas before wasting money and time on prototypes. On the other hand, the pioneers in the Disney research hub needed the supervised-learned, easily tunable simulators for their computer graphics simulations for physics-based animation. So, tada! An insightful simulator has been born. Let’s see what these guys did.
The behavior of a multibody system is sometimes hard to simulate since they consist of various rigid or elastic bodies with different characteristics and motion equations. The efficient dynamics solver is analytically differentiable. What does it mean? To overcome the difficulties of the non-smooth problem setting, the authors have proposed a differentiable simulator that combines fully implicit time stepping with a principled mollification of normal and tangential contact forces. These contact forces, as well as the coupled system mechanics of rigid and soft objects, are handled through a soft constraint formulation that is simple, numerically robust, and very effective. This formulation also allows us to analytically compute derivatives of simulation outcomes through adjoint sensitivity analysis.
The proposed frictional contact formulation applies to coupled rigid and deformable bodies in the multi-body system. Interestingly, our hybrid approach can be interpreted as the opposite of staggered projections as we often contact constraints with penalty forces but can enforce static friction with hard constraints.
In the context of identifying frictional parameters, we aim at characterizing material properties and initial conditions from motion capture (MoCap) data. For parameter estimation from MoCap, we draw inspiration from physics-guided reconstruction who considers frictionless contact between rigid bodies. Our formulation extends to frictional contact and deformable bodies.
The focus is on inverse dynamics. To enable design optimization, we have the goal of making our frictional contact model smooth and invertible with previous work in optimal control. Instead of relying on finite-differencing and explicit time integration, our approach builds on analytically-computed derivatives and fully implicit time integration, allowing us to handle both soft and stiff systems. Moreover, the proposed approach is an analytically differentiable simulator that handles frictional contact for rigid and deformable objects within a unified framework. The easy-to-tune characteristics of the model make it applicable to a wide range of inverse dynamics problems.
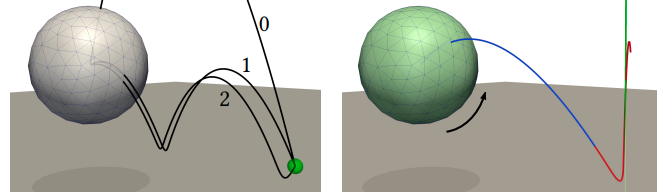
Throwing ball experiment:
The initial linear and angular velocities are optimized for throwing a deformable ball. The objective function measures the distance from the ball’s center of mass to a specific target or to a target line.
Bunny:
This experiment includes a bunny that contacts a wall. The objective function measures the squared distance
to the target pose for each mesh node, and also includes a regularize that additionally penalizes solutions where the bunny falls over.

To wrap up, the proposed approach would enable efficient inverse problem-solving. Also, we explore options for smoother friction forces, which help reduce noise in the objective function, as well as equality constraints. In addition, it enables differentiability and gradient-based optimization.