Today, let’s talk about perhaps one of the most intimdating graphics papers ever published (it perhaps even held the title of most intimidating at least until Albert Chern, et al. wrote Schrödinger’s Smoke in 2016). That’s right! This blog post is on Velocity-Based Shock Propagation for Multibody Dynamics Animation by Kenny Erleben. It was published on June 2007 in the venerated ACM Transactions on Graphics.
As you can tell from the title, the paper deals with multibody dynamics, a pivotal component in physics based animations, virtual prototyping, and games. In many of these applications, it even needs to be done in real time. A modern scene contains hundreds if not thousands of objects that are all capable of interacting with each other. In some cases, we can cheat and use textures to make it look like there are more objects than there really are. But sometimes, it really is necessary to deal with such a large number of them. And as time goes on, the applications are only increasing in complexity and scale.
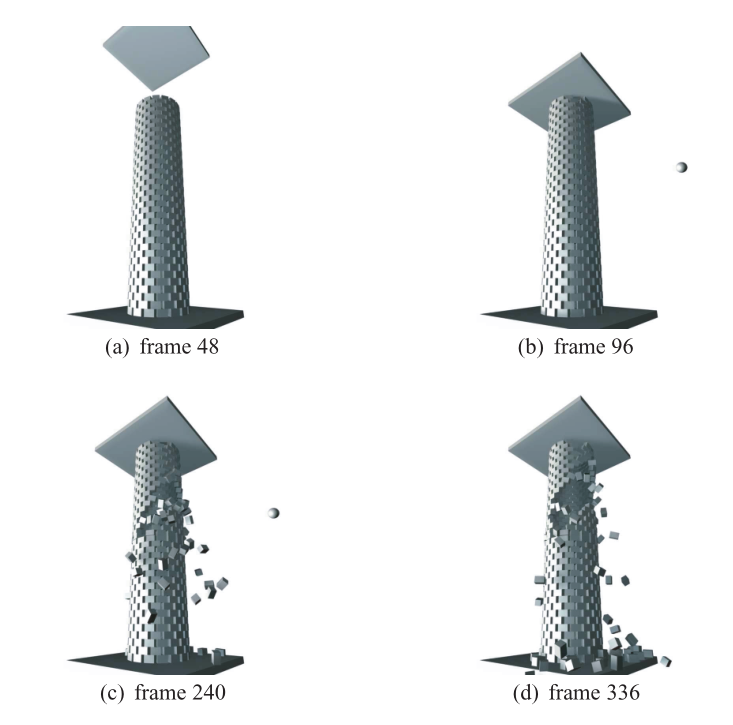
This paper presents a multibody dynamics scheme based on an explicit, fixed-time stepping scheme for velocity based formulation. It focuses on computing the dynamics for “large scale dense structured stacking at interactive frame rates”. Think simulating Jenga but massively scaled up.
A major problem of previous multibody dynamics methods was their inability to deal with dense structured stacking. The interesting thing about this problem is that it is completely unforgiving. If object populations are kept in some sparse system, then there are only a few constraints that need to be tracked. If there is no structure, then small mistakes in the dynamics calculations may go unnoticed. But in a well structured system? Mistakes will be obvious since they break the structure. And since it is dense, there are a lot more constraints to consider; a lot more places where things can go wrong. Even worse, the large number of constraints means that it is more likely that a few small errors will propagate into something catastropic. This restricted what kind of systems can be simulated even though strict physical accuracy is typically unnecessary in computer graphics.
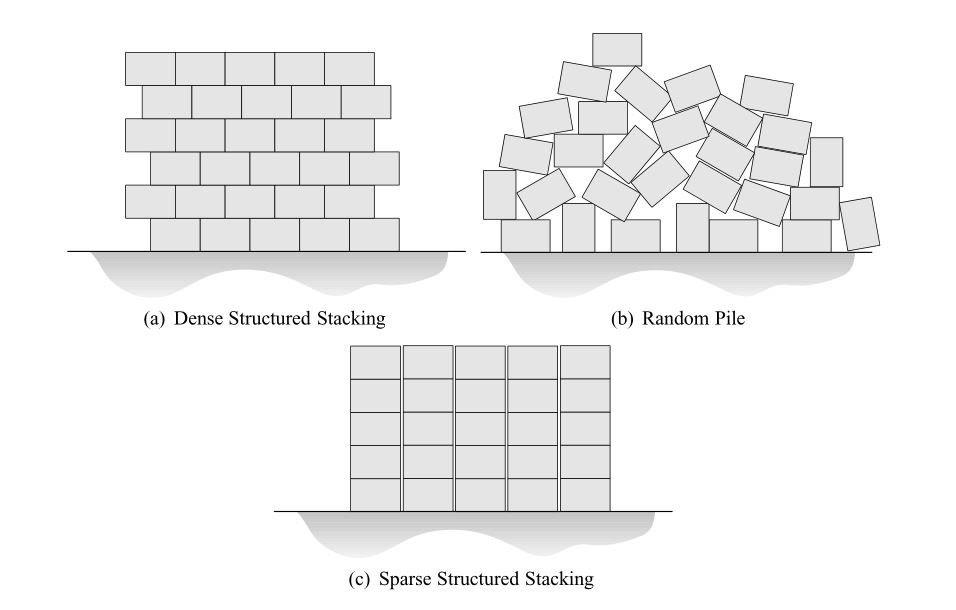
The importance of this paper is that it provides a method for efficiently dealing with the dynamics of very large, densely structured piles where none existed previously.
In section 2, the paper works through the velocity based complementarity method. In section 3, an iterative method is presented to be applied to the velocity based complementarity. In section 4, the dynamics problem is approached using a velocity based shock propagation method.
A complementarity problem is one where you have 2 variables, and wish to ensure that they always satisfy the complementarity constraint. The complementarity constraint reads that the product of the two non-negative numbers must be 0. So basically, when one variable is positive, the other must be 0. The complementarity problem is extended to become a linear complementarity problem with the addition of a linear relation between the two variables. This new type of problem has been very important historically in its relation to optimization problems. In graphics, it has been used for modelling contact forces. To learn more about the linear complementarity problem and its application in graphics, Kenny Erelben (the same guy who published this paper) wrote lecture notes on it for SIGGRAPH 2013.
Going back to the paper, our velocity complementarity problem is posed to handle contact. In particular, it is used to ensure that the normal force is repulsive and zero at separation. All very sensible when you want to simulate interacting objects. Solving this linear complementarity problem (which is done with the method presented in section 3) yields the values needed to proceed with the simulation as they are components in the equation of motion. From there, it’s straightforward enough – use a forward Euler step on the equation of motion to update the velocities. Ah, but now to earn that fearsome reputation, the final position update from the newly calculated velocities is done in a particularly fancy way incorporating Lagrange multipliers and quaternions.
Now that we’ve gone through the pains of formulating the problem to solve, we need to actually solve it. The iterative solver in section 3 was good for what it needed to do there, but may be really slow here. And since we want to apply this method to really huge scenes, it’s important to choose our solver carefully. The choice made here gives rise to the first half of the paper’s title: “Velocity-Based Shock Propagation.”
Shock propagation was a method initially developed by Guendelman et al. [2003]. Here, Erleben adapts it to be velocity based. The results are quite impressive – through all of his simulations containing several hundred objects densely structured, no more than 10 iterations were required to solve the dynamics! In this method, we first construct a contact graph so that for each object, we know how how many other objects (in immediate contact) need to be traversed to reach the nearest fixed body. This number of objects that need to be traversed is called a stack height. Next, we create stack layers. The i-th stack layer contains all of the objects with stack height of i and i+1 as well as the contact points between them. Constructing this is easy to do with a breadth first traversal. Now, we use this stack layer structure to apply the dynamics to the system in a particular order so that things don’t spontaneously explode. This is done by iterating through the stack layers in increasing order. In each stack layer, we fix the bottom most objects (meaning lowest stack height) in the layer, and apply our dyanmics to it.
By using the velocity based shock propagation to apply the dynamics to the system, we can resolve contact in such an order that things do not just fly apart. This allows for the stable simulation of some very interesting and complicated structures of objects.